Understansing the forward and backward pass of LSTM

Recurrent Neural Network(RNN) is a specific learning approach for the sequence generation. It is naturally applied in natural launguage processing(NLP), image captioning and time series prediction. One difficulty to train the RNN is that the gradient will be vanished in the Vanilla RNN, since the gradient of hidden state (\(h\)) involves many multiplication of the weight matrix(\(W\)). Long Short Term Memory neural network(LSTM) utilizes the gate mechanism to overcome the vanishing gradient problem.

In a nutshell

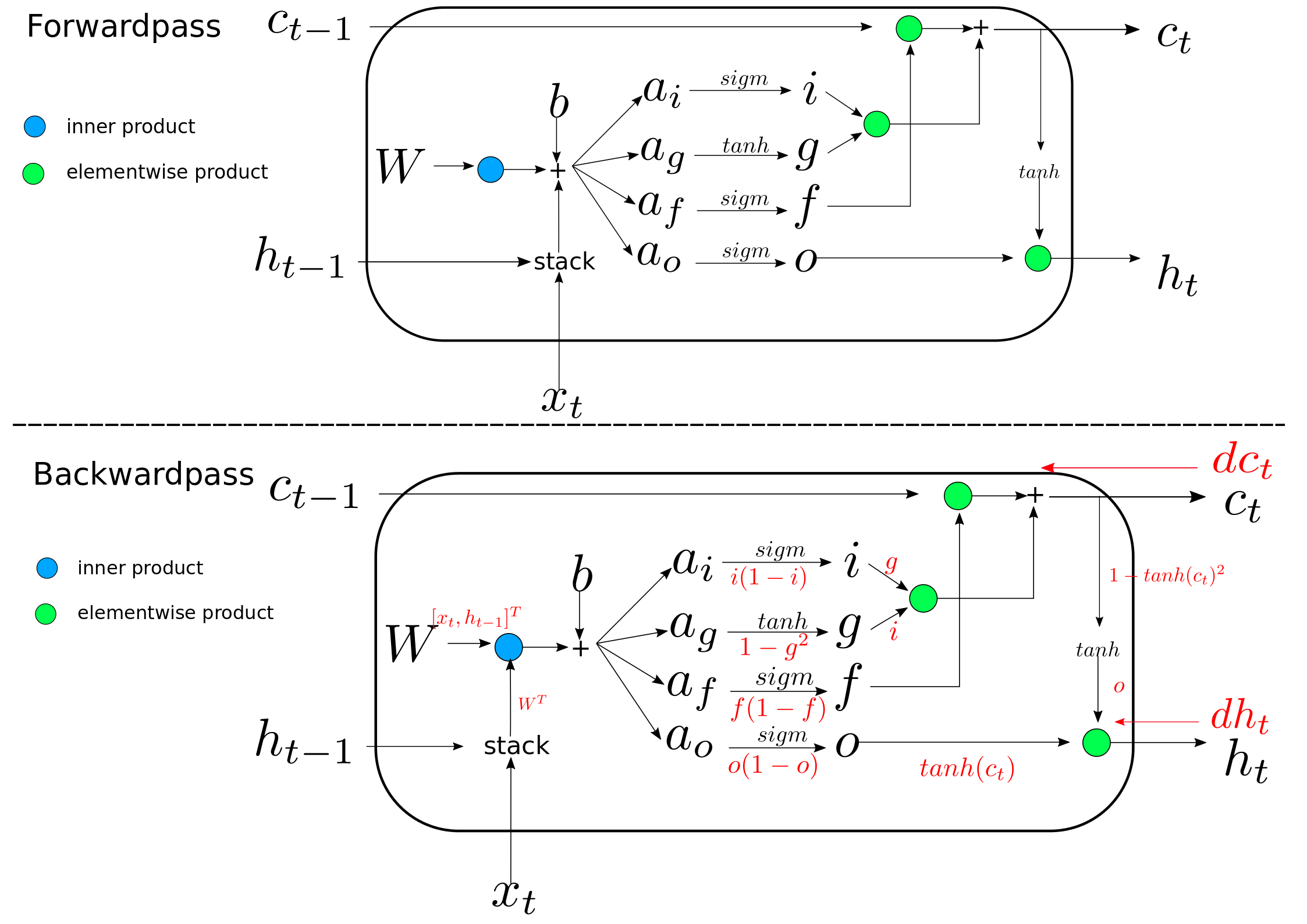
Forwardpass

As it is shown in the figure above, the space of the weight matrix is extended to four folds, which means \(W \in \mathbf{R}^{4H}\), where \(H\) is the normal space for the hidden state in Vanilla RNN. These four fold weight matrix is intentionally used for four gates including the input gate(\(i\)), output gate(\(o\)), forgetting gate(\(f\)) and block input(\(g\)).

Backwardpass

The argument for LSTM to avoid the vanishing gradient problem is that the gradeint of previous cell state(\(c_{t-1}\)) doesn’t involve the factor of the weight matrix \(W\). The overall backward computation graph is shown as red functions in the figure. The red functions show the gradient flow at every step.

The python code is:

def lstm_step_backward(dnext_h, dnext_c, cache):
    """
    Backward pass for a single timestep of an LSTM.

    Inputs:
    - dnext_h: Gradients of next hidden state, of shape (N, H)
    - dnext_c: Gradients of next cell state, of shape (N, H)
    - cache: Values from the forward pass

    Returns a tuple of:
    - dx: Gradient of input data, of shape (N, D)
    - dprev_h: Gradient of previous hidden state, of shape (N, H)
    - dprev_c: Gradient of previous cell state, of shape (N, H)
    - dWx: Gradient of input-to-hidden weights, of shape (D, 4H)
    - dWh: Gradient of hidden-to-hidden weights, of shape (H, 4H)
    - db: Gradient of biases, of shape (4H,)
    """
    dx, dprev_h, dprev_c, dWx, dWh, db = None, None, None, None, None, None
    
    i,f,o,g,next_c, prev_c,x, prev_h, Wx, Wh = cache
    N,D = x.shape
    dnext_h_next_c = (1-np.tanh(next_c)**2)*o*dnext_h
    dprev_c_next_c = f*dnext_c
    dprev_c_next_h = f*dnext_h_next_c

    dprev_c = dprev_c_next_c+dprev_c_next_h

    dai_next_c = i*(1-i)*g*(dnext_c+dnext_h_next_c)
    daf_next_c = f*(1-f)*prev_c*(dnext_c+dnext_h_next_c)
    dao_next_h = o*(1-o)*np.tanh(next_c)*dnext_h
    dag_next_c = (1-g**2)*i*(dnext_c+dnext_h_next_c)

    stack = np.concatenate((x, prev_h), axis=1)
    d_activation = np.concatenate((dai_next_c, daf_next_c, dao_next_h, dag_next_c), axis=1)
    dW = np.dot(stack.T,d_activation)
    dWx = dW[:D,:]
    dWh = dW[D:,:]
    db = np.sum(d_activation,axis=0)

    W = np.concatenate((Wx, Wh), axis=0)
    dxh = np.dot(d_activation, W.T)
    dx = dxh[:,:D]
    dprev_h = dxh[:,D:]

    return dx, dprev_h, dprev_c, dWx, dWh, db